3 Amazing ways to generate random numbers without Math.random()

Have you ever played an online spin to win game? You know! The one that pops up as an Ad with the message “Spin this to win the latest, feature-rich Samsung smartphone!”? I did. Because who doesn’t want the latest smartphone for free? Sadly, no matter how many times I played, I didn’t win. Never the less, I was rewarded. Rewarded with the curiosity to know how this deceitful game worked. With a quick google search, I found that it worked by using a random number generator (RNG). It’s probably Math.random()

But… How does a computer, a device that is designed to work as per the instructions given by a human generate random numbers? Answer, it doesn’t. And it can’t. That is why it’s called a “pseudo” random number generator (PRNG). It means it’s a fake. It’s a knock-off.

Why a knock-off?

A True RNG needs additional hardware that can use real-world random phenomena from throwing dice 🎲 to measuring radiation from a radioactive material as an input to generate random numbers. Wow! Using the randomness in radioactive decay just to generate a number is mind-blowing! 🤯 Take a moment to let that sink in.

But this additional hardware is costly and who would willingly carry a radioactive material in their pockets except for Lex Luthor? That is why everyone agreed to settle with a PRNG.

Superman: The Animated Series, © Warner Bros Animation, 1996

PRNG is not a single standard algorithm used everywhere. I was struck dumb when I found out that there are not 1, not 2 but 28 different algorithms created by very smart people over the past 7 decades.

Let me show you 3 amazing ways to replace Math.random() in Javascript.

How do they work?

Pseudo Random Number Generator (PRNG) refers to an algorithm that uses mathematical formulas to produce sequences of random numbers.

https://www.geeksforgeeks.org/pseudo-random-number-generator-prng/

Though I couldn’t research all the 28 algorithms in a short time, I looked up 3 good ones. I first thought they used complex mathematical derivatives involving 100s of lines of code. Nope! I was wrong. With 2 to 5 lines of code involving basic arithmetic operations, they’re unbelievably simple. This makes it easier for beginners to understand.

All 3 algorithms and PRNGs, in general, followed these common steps

1. All these algorithms accept an input called the seed 🌱 number. This is the base number on which the formula is applied. Some algorithms can take other inputs as required by the mathematical operation to be performed.

2. They, then apply the inputs on the formula and the result generated is the random number.

3. The generated number is used as the seed for the next run.

4. These steps are repeated to create a sequence of numbers that make us believe they are random.

An unique property that separates PRNGs from true RNGs is that the sequences generated by PRNGs inevitably repeat themselves at one point of time.

Avengers: Endgame, © Marvel Studios, 2019

1. Middle square method (MSM)

Invented by John von Neumann and described in 1946, the Middle Square Method (MSM) is the first-ever method designed to generate pseudo-random number sequences ^[1]. Implementing this method is a child’s play. For an n-digit random number sequence,

1. Start with an n-digit number as the seed. Let’s say it’s a 2-digit number 42.

2. Square it. Here, the square of 42 is 1764.

3. Extract the middle n-digits of the squared number to get the next number in our sequence. In our case, the next number would be 76.

4. Use the result as the seed and repeat steps 1-4 for the next cycle.

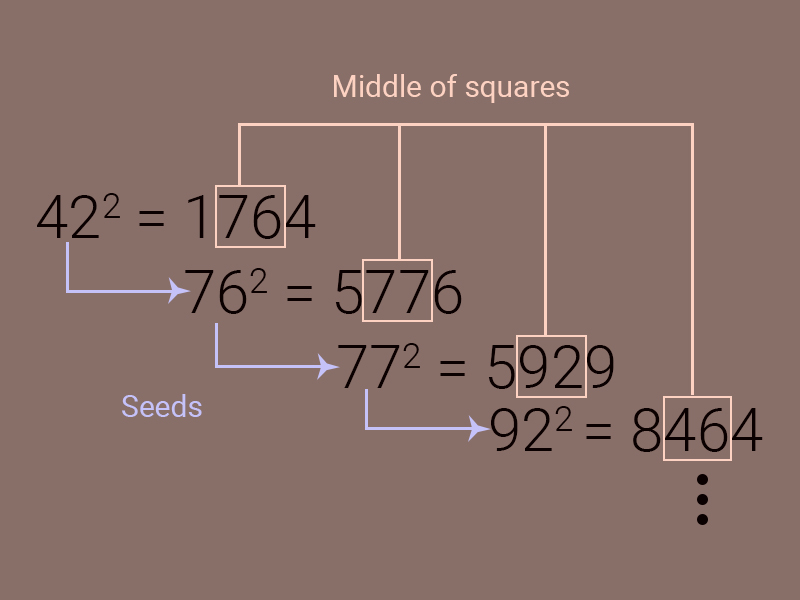Representation of middle square method

The simple nature of the algorithm is used as an exercise for beginner programmers to check their knowledge in the language they learned in Bootcamp. So, here’s my implementation in JS to help them.

/**

* Middle Square Method implementation in JavaScript

* for a 2-digit random number sequence

**/

var seed;

function middleSquareMethod(){

    var result = (seed * seed).toString().slice(1, 3); // extracting the middle value.

    seed = parseInt(result);

    return parseInt(result);

}

There is a problem with this approach. There are exceptional numbers whose square value have odd digits which makes it difficult to extract the middle digits like in the case of 15. Squaring 15 would result in 225. And we cannot accept 2 as the middle number since we need two digits. To solve this, we pad zeroes in front of the square value to make it even digits. Now 225 becomes 0225 which makes it easy to extract the middle 2 digits which is 22. After rectifying the problem, the code looks like this.

/**

* Middle Square Method implementation in JavaScript

* for a 2-digit random number sequence

**/  

var seed = 42;

function middleSquareMethod(){

    var result = (seed * seed).toString().padStart(4,"0").slice(1, 3);
    // pad with zero when necessary and extract the middle value.

    seed = parseInt(result);

    return parseInt(result);

}

With just three lines of code, we could generate a maximum of 8ⁿ numbers for an n-digit number after which the sequence repeats itself. There is a pitfall though. Some seeds can cause the algorithm to have a shorter cycle like the seed 25, which causes the algorithm to repeat 25 indefinitely.

2. The Linear Congruential Generator (LCG) algorithm

This fascinating algorithm uses more math than MSM. The LCG uses a linear equation that involves congruence operation for the generation of a random sequence of numbers. “Whoa! What’s all these fancy terms?” I can hear you exclaiming. Let me explain.

Linear means an algebraic equation that has no variables raised to the power greater than one.

Congruential means an equation that uses modulus division operation.

With its jargons, the algorithm might seem sophisticated. But, it’s very simple to understand as it uses very basic algebra and arithmetic operations. It uses this particular equation X_n+1 = (aX_n + c) mod m. Alright! Alright! No more math terms. I’ll translate it to programmer readable from. The translated equation is, X = (a * X + c) % m

Where X is the seed. Akin to the MSM the result is used as the seed for the next cycle.

a – is the multiplier

c – is the increment and

m – is the modulus

It has the following conditions

1. m > 0, duh! divide by zero is impossible

2. 0 < a < m

3. 0 ≤ c < m and

4. 0 ≤ X < m

Since this is a simple equation, solving this is a piece of cake for computers. In the case of the MSM, data conversion from number to string and back to number is required, which are heavy on the CPU. For this reason, LCG is the oldest and best-known random number generator algorithm ^[2]. And hence takes 2^nd in the list.

After all, both the increment and the seed can take the value zero care should be taken that both do not take zero or else it just spits out a sequence of zeroes.

Here’s how I wrote the LCG in JS

/**
* Implementation of the Linear congruential generator
* algorithm in JavaScript
*/
var X,a,c,m;

function linearCongruentialGenerator(){

    X = (a * X + c) % m;

    return X;

}

It takes just two lines. Just two! I did a double-take after writing it 😲. It’s really incredible to see a simple equation to achieve something this big. This just increased my respect for Math.

With the right combination of inputs, we could generate a very long sequence. Longer than the MSM before it starts repeating itself. In my example I used the values a = 1664525, m = 2³² and c = 1013904223 as used in Numerical Recipes ^[3].

3. Xorshift algorithm

The third algorithm in the list is the Xorshift algorithm. I’ve saved this special one for the last. If the MSM is easier to understand for humans and the LCG is understandable by both humans and computers then the XOR shift algorithm is easily understandable only to computers. Because this method, as the name suggests, uses the special and rarely used binary operations Xor and bit shift.

Please bear with me. This one uses a lot of computer science terms. I chose this one because I thought I would never get to use those binary operators in my life just like how I thought I could never see Ash Ketchum win the Pokémon league championship.

Let me break down the algorithm. Bit shifting works by shifting the bits in the binary number either to the left or right. The result is a completely different number. For 1-bit shift to left, each bit is shifted one place to the left. The empty space is filled with 0 and the shifted out bit is discarded. And for a 5-bit shift to the left, single-bit shift operation is repeated 5 times. Here is an example:

The binary equivalent of 42₁₀ in a 16-bit representation is 0000000000101010₂.
After shifting 5 bits to the left it becomes 0000010101000000₂ which is the binary equivalent of 1344₁₀.

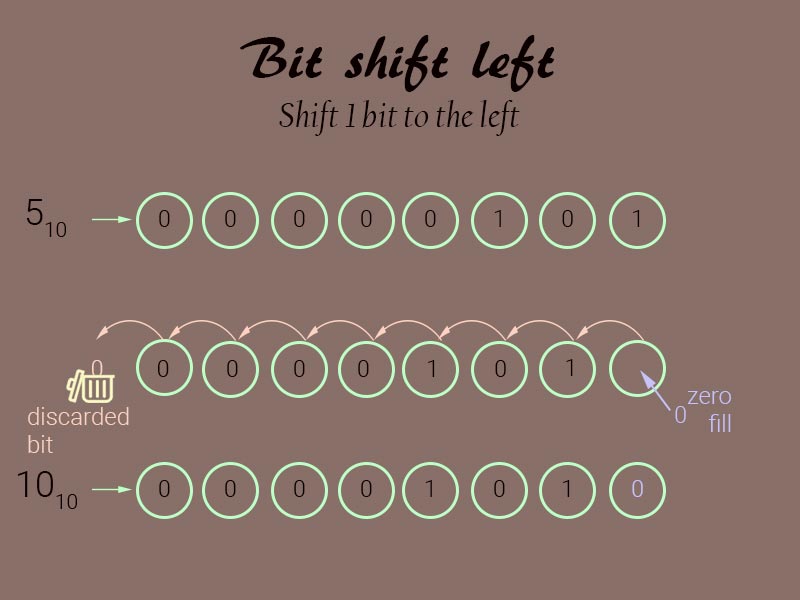Representation of 1-bit shift left operation in a 8 bit system

And if we shift the binary equivalent of 2524₁₀ – 0000100111011100₂ 5 bits to the right it becomes 0000000001001110₂ which is 78₁₀ in decimal. The rest of the bits on the right side is discarded.

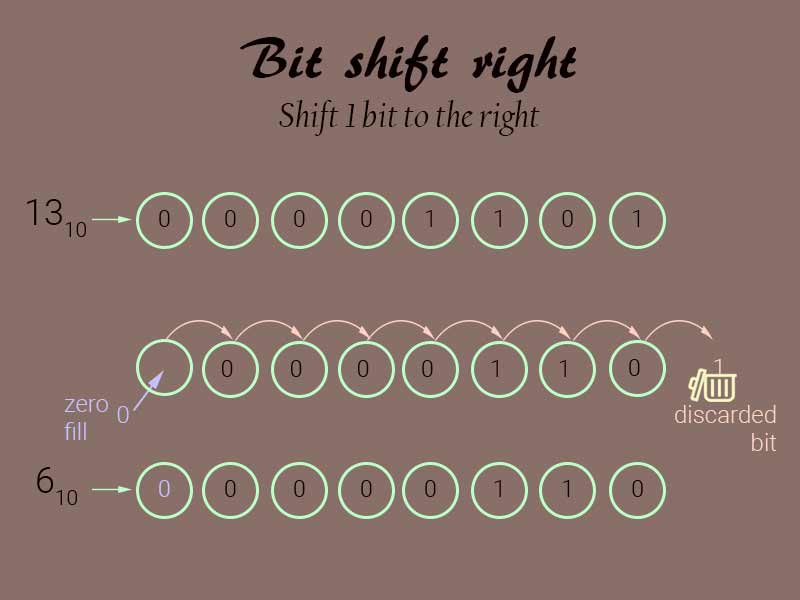Representation of 1-bit shift right operation in a 8 bit system

The bit shift operation, as you can see, requires only one operand and the result is a completely different number. On the other hand, the Xor operation requires two operands. XOR short for Exclusive OR operation compares the bits of two binary numbers and sets the bit of the result to 1 only when one of the bits in comparison is 1. Continuing with the previous example the Xor of 42 and 2524 takes place like this:

4210 – 0000000000101010₂

252410 – 0000100111011100₂ XOR - 0000100111110110₂ which is the equivalent of 2550₁₀.

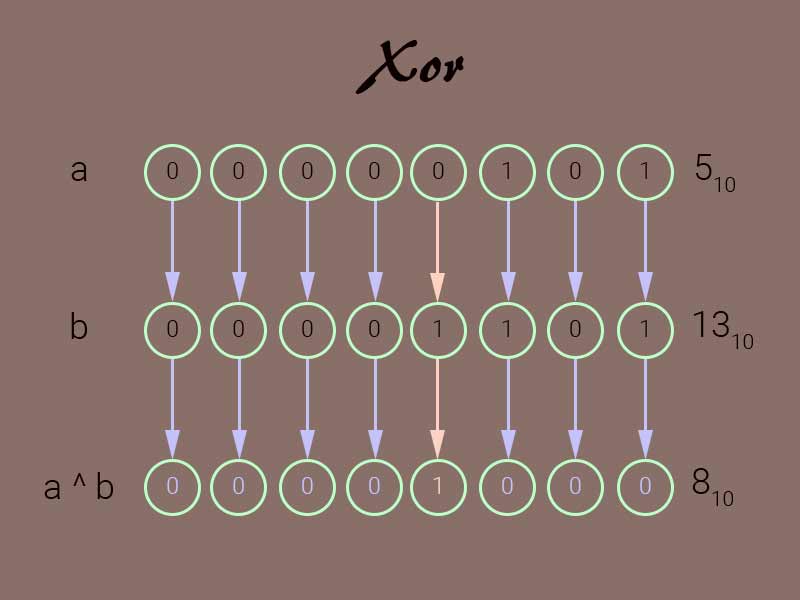Representation of xor operation in a 8 bit system

Xor also results in a different number. This algorithm combines the power of these two operations. And, here is my implementation of Xorshift in JavaScript.

/**
* Implementation of XorShift
* algorithm in JavaScript
*/
var seed;

function xorShift(){

  seed ^= seed << 13;

  seed ^= seed >> 17;

  seed ^= seed << 5;

  return seed;
}

This method performs consecutive bits shifts and Xor operations on the seed which creates a random sequence containing both positive and negative numbers. The constants 13, 17 and 5 in the algorithm is from the list of triplets suggested in the paper describing the Xor-shift algorithm ⁴. This algorithm works directly in binary, the language of the computers, which makes it faster than the LCG.

If you want only positive numbers, you can take the 2’s complement of the seed if it’s negative before returning the value. This can reduce the performance with the inclusion of a condition.

/**
* Implementation of XorShift
* algorithm in JavaScript
* with 2's complement
*/
function xorShift(){

  seed ^= seed << 13;

  seed ^= seed >> 17;

  seed ^= seed << 5;

  return (seed <0)?~seed+1: seed; //2's complement of the negative result to make all numbers positive.
}

Computers store the positive and negative numbers (called signed integers) as binary numbers in 2’s compliment from. The leftmost bit (the most significant bit) is reserved to represent the sign of the number. 0 represents a positive (+) sign and 1 stands for negative (-) sign.

Do you know what a two’s complement is? Don’t worry I’ll explain.

In 2’s complement, A binary number say 11111111 11010011 (-45₁₀) is taken and its bits are flipped. Meaning, 0s are made to 1s and vice versa. And finally, 1₂ is added to the flipped number. The result 00000000 00101101₂,is the positive form of the number (45₁₀).

-45₁₀ ➡ 11111111 11010011₂

Bit inversion

00000000 00101100₂

Add 1

00000000 00101100₂ + 1₂

00000000 00101101₂ ➡ 45₁₀

Thus, in our algorithm, we always end up with positive numbers.

Conclusion

This article is just the tip of the iceberg in the rabbit hole of PRNGs. I wanted to share you the different ways to replace Math.random(). All these samples give out whole numbers which is the complete opposite of Math.random(). Math.random() spits out random decimal numbers only between 0 and 1. I’ll leave the conversion as an exercise to you. You can use ES5 features like generator functions to implement these. If someone does that, please post it in the comments.

Thanks for reading 😊

References

• ^[1] “List of pseudo random number generators”, Wikipedia.

• ^[2][3] “Linear congruential generator”, Wikipedia.

• ^[4] “Xorshift RNGs” [pdf] by Marsaglia, George, The journal of statistical software.

Cover image credit: Image by PIRO4D from Pixabay

• ← Previous Post
• Next Post →